100人の送受信者が共通鍵暗号方式で、それぞれ秘密に通信を行うときに必要な暗号鍵の総数は幾つか。
ア 100
イ 200
ウ 4,950
エ 9,900
共通鍵暗号方式を用いる場合、鍵はいくつ必要か、という問題。
問題の解説
共通鍵暗号の場合、通信を行うペアひとつにつき、鍵も一つ必要になる。したがって、「100人の中から2人でペアを作る場合、何パターンのペアが存在するか」を考えれば答えは出る。これは組み合わせの公式をそのまま使えば求めることができる。
$${}_{100}C_{2} =\frac{100\times99}{2} = 4950$$
という事で4950が答えとなる(ウ)
公式っぽく書いてみると、
$${}_{n}C_{2} =\frac{n\times(n-1)}{2} = 0.5n(n-1)$$
n:送受信者の数
公開鍵暗号の場合に必要な鍵数
せっかくなので、公開鍵暗号についても考えてみる。
公開鍵暗号の場合、公開鍵は受信者1人に対して送信者99人は同じ公開鍵を用いる。そのため、受信者一人につき、公開鍵と秘密鍵が1つずつ必要になる。
先ほどの問題と同じ条件(送受信者100人)の場合
100×2 = 200[個]
ということで、200個の鍵(秘密鍵100個、公開鍵100個)が必要になる。
こちらも公式っぽくしてみると、
2n
n:送受信者の数
となる。シンプルすぎて余白が多い。
共通鍵暗号方式と公開鍵暗号方式の鍵数の比較
二つの公式を並べてみよう。
公開鍵暗号方式の鍵数:2n[個]
共通鍵暗号方式の鍵数:0.5n(n-1)[個]
公開鍵暗号方式はO(n)のオーダーで鍵数が増えるのに対し、共通鍵暗号方式の場合はO(n2)のオーダーで鍵数が増える。そのため、共通鍵暗号方式は、送受信者の人数が増えると鍵管理が複雑になるというデメリットがある。
具体的な数値をいくつか代入して試してみよう。
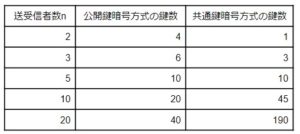
グラフも作ってみた。
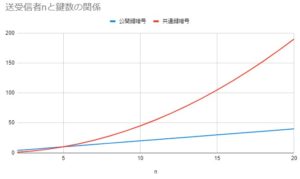
グラフと表を見てみると、送受信者数が4人以下の場合、共通鍵暗号方式のほうが鍵数が少ないが、5人になると同じ数となり、6人以上になると共通鍵暗号方式のほうが鍵数が多くなることがわかる。nが大きくなるほど必要な鍵数の差はものすごい勢いで開いていく。
こういったデータを見てもわかる通り、送受信者が2~3人の限られた者同士の通信には共通鍵暗号方式が向いているが、人数が多い場合は公開鍵暗号方式のほうが向いているといえる。
特に送信者が多数で受信者が一人の場合、公開鍵暗号方式は向いている。この場合はひとつの公開鍵で何人からでも受信できる。
暗号方式の鍵数:まとめ
- 共通鍵暗号方式の鍵数はnを送受信者数とすると、0.5n(n-1)個となる。
- 公開鍵暗号方式の鍵数は2n個となる。
- 共通鍵方式は送受信者の人数が増えると鍵管理が面倒になるというでデメリットがあり、限られた者同士での通信に向く。
- 公開鍵暗号方式は、送受信者数が多くても鍵数が大きく増えない。
- 公開鍵暗号方式は送信者が多数で受信者が一人という場合に特に向いている。
類題 公開鍵暗号方式の鍵数に関する問題

応用情報の問題だが、これもこのページに書いてある知識だけで解ける。というか公式そのもの。応用情報の過去問が情報処理安全確保支援試験に登場することはよくあるので、資格勉強をしている人は目を通しておくといいかもしれない。